九色国产,午夜在线视频,新黄色网址,九九色综合,天天做夜夜做久久做狠狠,天天躁夜夜躁狠狠躁2021a,久久不卡一区二区三区

This tutorial is intended for readers who are new to both machine learning andTensorFlow. If you already know what MNIST is, and what softmax (multinomiallogistic) regression is, you might prefer thisfaster paced tutorial. Be sure toinstall TensorFlow before starting eithertutorial.

When one learns how to program, there's a tradition that the first thing you dois print "Hello World." Just like programming has Hello World, machine learninghas MNIST.

MNIST is a simple computer vision dataset. It consists of images of handwrittendigits like these:

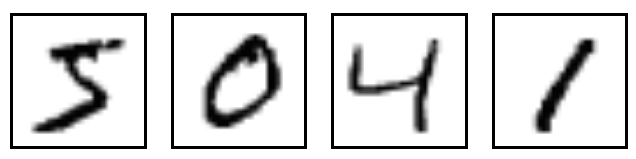
It also includes labels for each image, telling us which digit it is. Forexample, the labels for the above images are 5, 0, 4, and 1.

In this tutorial, we're going to train a model to look at images and predictwhat digits they are. Our goal isn't to train a really elaborate model thatachieves state-of-the-art performance -- although we'll give you code to do thatlater! -- but rather to dip a toe into using TensorFlow. As such, we're goingto start with a very simple model, called a Softmax Regression.

The actual code for this tutorial is very short, and all the interestingstuff happens in just three lines. However, it is veryimportant to understand the ideas behind it: both how TensorFlow works and thecore machine learning concepts. Because of this, we are going to very carefullywork through the code.

About this tutorial

This tutorial is an explanation, line by line, of what is happening in themnist_softmax.py code.

You can use this tutorial in a few different ways, including:

• Copy and paste each code snippet, line by line, into a Python environment as you read through the explanations of each line.

• Run the entire mnist_softmax.py Python file either before or after reading through the explanations, and use this tutorial to understand the lines of code that aren't clear to you.

What we will accomplish in this tutorial:

• Learn about the MNIST data and softmax regressions

• Create a function that is a model for recognizing digits, based on looking at every pixel in the image

• Use Tensorflow to train the model to recognize digits by having it "look" at thousands of examples (and run our first Tensorflow session to do so)

• Check the model's accuracy with our test data

The MNIST Data

The MNIST data is hosted onYann LeCun's website. If you are copying andpasting in the code from this tutorial, start here with these two lines of codewhich will download and read in the data automatically:

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

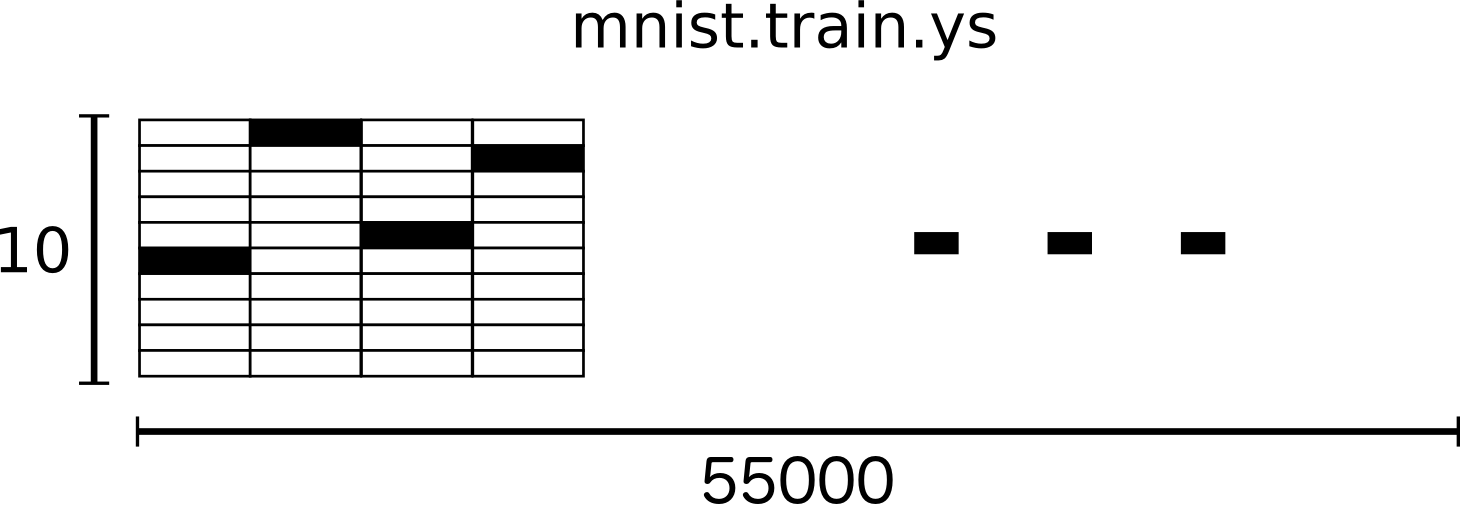
The MNIST data is split into three parts: 55,000 data points of trainingdata (mnist.train), 10,000 points of test data (mnist.test), and 5,000points of validation data (mnist.validation). This split is very important:it's essential in machine learning that we have separate data which we don'tlearn from so that we can make sure that what we've learned actuallygeneralizes!

As mentioned earlier, every MNIST data point has two parts: an image of ahandwritten digit and a corresponding label. We'll call the images "x"and the labels "y". Both the training set and test set contain images and theircorresponding labels; for example the training images are mnist.train.imagesand the training labels are mnist.train.labels.

Each image is 28 pixels by 28 pixels. We can interpret this as a big array ofnumbers:

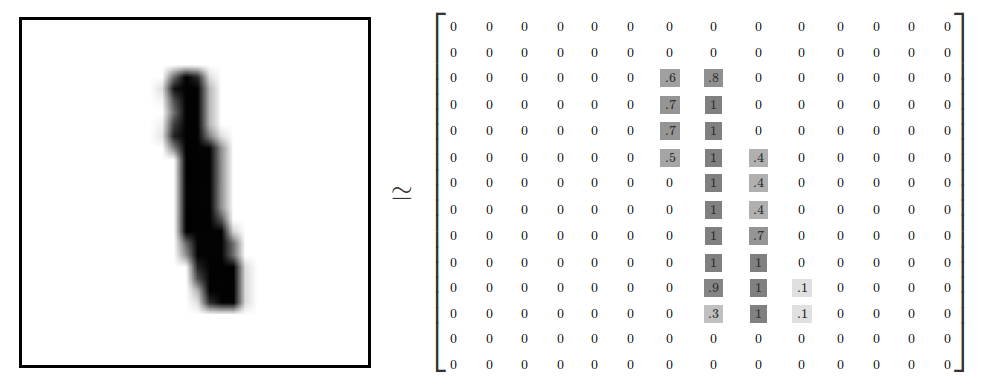
We can flatten this array into a vector of 28x28 = 784 numbers. It doesn'tmatter how we flatten the array, as long as we're consistent between images.From this perspective, the MNIST images are just a bunch of points in a784-dimensional vector space, with avery rich structure(warning: computationally intensive visualizations).

Flattening the data throws away information about the 2D structure of the image.Isn't that bad? Well, the best computer vision methods do exploit thisstructure, and we will in later tutorials. But the simple method we will beusing here, a softmax regression (defined below), won't.

The result is that mnist.train.images is a tensor (an n-dimensional array)with a shape of [55000, 784]. The first dimension is an index into the listof images and the second dimension is the index for each pixel in each image.Each entry in the tensor is a pixel intensity between 0 and 1, for a particularpixel in a particular image.

Each image in MNIST has a corresponding label, a number between 0 and 9representing the digit drawn in the image.

For the purposes of this tutorial, we're going to want our labels as "one-hotvectors". A one-hot vector is a vector which is 0 in most dimensions, and 1 in asingle dimension. In this case, the $n$th digit will be represented as avector which is 1 in the $n$th dimension. For example, 3 would be$[0,0,0,1,0,0,0,0,0,0]$. Consequently, mnist.train.labels is a[55000, 10] array of floats.

We're now ready to actually make our model!

Softmax Regressions

We know that every image in MNIST is of a handwritten digit between zero andnine. So there are only ten possible things that a given image can be. We wantto be able to look at an image and give the probabilities for it being eachdigit. For example, our model might look at a picture of a nine and be 80% sureit's a nine, but give a 5% chance to it being an eight (because of the top loop)and a bit of probability to all the others because it isn't 100% sure.

This is a classic case where a softmax regression is a natural, simple model.If you want to assign probabilities to an object being one of several differentthings, softmax is the thing to do, because softmax gives us a list of valuesbetween 0 and 1 that add up to 1. Even later on, when we train more sophisticatedmodels, the final step will be a layer of softmax.

A softmax regression has two steps: first we add up the evidence of our inputbeing in certain classes, and then we convert that evidence into probabilities.

To tally up the evidence that a given image is in a particular class, we do aweighted sum of the pixel intensities. The weight is negative if that pixelhaving a high intensity is evidence against the image being in that class, andpositive if it is evidence in favor.

The following diagram shows the weights one model learned for each of theseclasses. Red represents negative weights, while blue represents positiveweights.

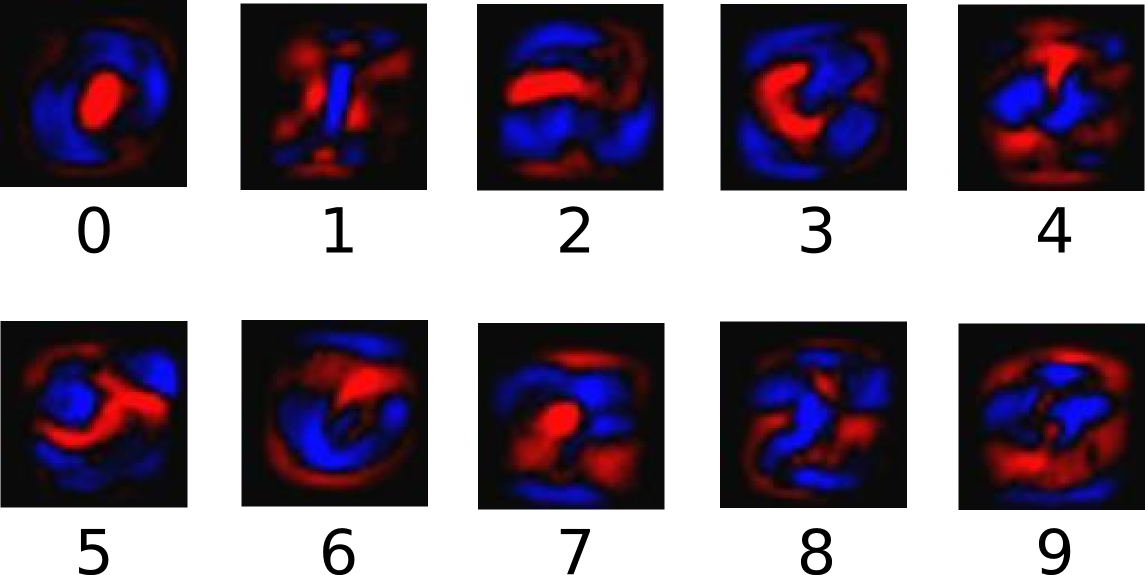
We also add some extra evidence called a bias. Basically, we want to be ableto say that some things are more likely independent of the input. The result isthat the evidence for a class $i$ given an input $x$ is:

where $W_i$ is the weights and $b_i$ is the bias for class $i$,and $j$ is an index for summing over the pixels in our input image $x$.We then convert the evidence tallies into our predicted probabilities$y$ using the "softmax" function:

Here softmax is serving as an "activation" or "link" function, shapingthe output of our linear function into the form we want -- in this case, aprobability distribution over 10 cases.You can think of it as converting talliesof evidence into probabilities of our input being in each class.It's defined as:

If you expand that equation out, you get:

But it's often more helpful to think of softmax the first way: exponentiatingits inputs and then normalizing them. The exponentiation means that one moreunit of evidence increases the weight given to any hypothesis multiplicatively.And conversely, having one less unit of evidence means that a hypothesis gets afraction of its earlier weight. No hypothesis ever has zero or negativeweight. Softmax then normalizes these weights, so that they add up to one,forming a valid probability distribution. (To get more intuition about thesoftmax function, check out thesection on it inMichael Nielsen's book, complete with an interactive visualization.)

You can picture our softmax regression as looking something like the following,although with a lot more $x$s. For each output, we compute a weighted sum ofthe $x$s, add a bias, and then apply softmax.

If we write that out as equations, we get:

We can "vectorize" this procedure, turning it into a matrix multiplicationand vector addition. This is helpful for computational efficiency. (It's alsoa useful way to think.)

More compactly, we can just write:

Now let's turn that into something that Tensorflow can use.

Implementing the Regression

To do efficient numerical computing in Python, we typically use libraries likeNumPy that do expensive operations such as matrixmultiplication outside Python, using highly efficient code implemented inanother language. Unfortunately, there can still be a lot of overhead fromswitching back to Python every operation. This overhead is especially bad if youwant to run computations on GPUs or in a distributed manner, where there can bea high cost to transferring data.

TensorFlow also does its heavy lifting outside Python, but it takes things astep further to avoid this overhead. Instead of running a single expensiveoperation independently from Python, TensorFlow lets us describe a graph ofinteracting operations that run entirely outside Python. (Approaches like thiscan be seen in a few machine learning libraries.)

To use TensorFlow, first we need to import it.

import tensorflow as tf

We describe these interacting operations by manipulating symbolic variables.Let's create one:

x = tf.placeholder(tf.float32, [None, 784])

x isn't a specific value. It's a placeholder, a value that we'll input whenwe ask TensorFlow to run a computation. We want to be able to input any numberof MNIST images, each flattened into a 784-dimensional vector. We representthis as a 2-D tensor of floating-point numbers, with a shape [None, 784].(Here None means that a dimension can be of any length.)

We also need the weights and biases for our model. We could imagine treatingthese like additional inputs, but TensorFlow has an even better way to handleit: Variable. A Variable is a modifiable tensor that lives in TensorFlow'sgraph of interacting operations. It can be used and even modified by thecomputation. For machine learning applications, one generally has the modelparameters be Variables.

W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))

We create these Variables by giving tf.Variable the initial value of theVariable: in this case, we initialize both W and b as tensors full ofzeros. Since we are going to learn W and b, it doesn't matter very muchwhat they initially are.

Notice that W has a shape of [784, 10] because we want to multiply the784-dimensional image vectors by it to produce 10-dimensional vectors ofevidence for the difference classes. b has a shape of [10] so we can add itto the output.

We can now implement our model. It only takes one line to define it!

y = tf.nn.softmax(tf.matmul(x, W) + b)

First, we multiply x by W with the expression tf.matmul(x, W). This isflipped from when we multiplied them in our equation, where we had $Wx$, asa small trick to deal with x being a 2D tensor with multiple inputs. We thenadd b, and finally apply tf.nn.softmax.

That's it. It only took us one line to define our model, after a couple shortlines of setup. That isn't because TensorFlow is designed to make a softmaxregression particularly easy: it's just a very flexible way to describe manykinds of numerical computations, from machine learning models to physicssimulations. And once defined, our model can be run on different devices:your computer's CPU, GPUs, and even phones!

Training

In order to train our model, we need to define what it means for the model to begood. Well, actually, in machine learning we typically define what it means fora model to be bad. We call this the cost, or the loss, and it represents how faroff our model is from our desired outcome. We try to minimize that error, andthe smaller the error margin, the better our model is.

One very common, very nice function to determine the loss of a model is called"cross-entropy." Cross-entropy arises from thinking about informationcompressing codes in information theory but it winds up being an important ideain lots of areas, from gambling to machine learning. It's defined as:

Where $y$ is our predicted probability distribution, and $y^{\prime }$ is the truedistribution (the one-hot vector with the digit labels). In some rough sense, thecross-entropy is measuring how inefficient our predictions are for describingthe truth. Going into more detail about cross-entropy is beyond the scope ofthis tutorial, but it's well worthunderstanding.

To implement cross-entropy we need to first add a new placeholder to input thecorrect answers:

y_ = tf.placeholder(tf.float32, [None, 10])

Then we can implement the cross-entropy function, $?\sum y^{\prime }\log ?(y)$:

cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))

First, tf.log computes the logarithm of each element of y. Next, we multiplyeach element of y_ with the corresponding element of tf.log(y). Thentf.reduce_sum adds the elements in the second dimension of y, due to thereduction_indices=[1] parameter. Finally, tf.reduce_mean computes the meanover all the examples in the batch.

(Note that in the source code, we don't use this formulation, because it isnumerically unstable. Instead, we applytf.nn.softmax_cross_entropy_with_logits on the unnormalized logits (e.g., wecall softmax_cross_entropy_with_logits on tf.matmul(x, W) + b), because thismore numerically stable function internally computes the softmax activation. Inyour code, consider using tf.nn.(sparse_)softmax_cross_entropy_with_logitsinstead).

Now that we know what we want our model to do, it's very easy to have TensorFlowtrain it to do so. Because TensorFlow knows the entire graph of yourcomputations, it can automatically use thebackpropagation algorithm toefficiently determine how your variables affect the loss you ask it tominimize. Then it can apply your choice of optimization algorithm to modify thevariables and reduce the loss.

train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

In this case, we ask TensorFlow to minimize cross_entropy using thegradient descent algorithmwith a learning rate of 0.5. Gradient descent is a simple procedure, whereTensorFlow simply shifts each variable a little bit in the direction thatreduces the cost. But TensorFlow also providesmany other optimization algorithms:using one is as simple as tweaking one line.

What TensorFlow actually does here, behind the scenes, is to add new operationsto your graph which implement backpropagation and gradient descent. Then itgives you back a single operation which, when run, does a step of gradientdescent training, slightly tweaking your variables to reduce the loss.

Now we have our model set up to train. One last thing before we launch it, wehave to create an operation to initialize the variables we created. Note thatthis defines the operation but does not run it yet:

init = tf.global_variables_initializer()

We can now launch the model in a Session, and now we run the operation thatinitializes the variables:

sess = tf.Session()
sess.run(init)

Let's train -- we'll run the training step 1000 times!

for i in range(1000):
  batch_xs, batch_ys = mnist.train.next_batch(100)
  sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

Each step of the loop, we get a "batch" of one hundred random data points fromour training set. We run train_step feeding in the batches data to replacethe placeholders.

Using small batches of random data is called stochastic training -- in thiscase, stochastic gradient descent. Ideally, we'd like to use all our data forevery step of training because that would give us a better sense of what weshould be doing, but that's expensive. So, instead, we use a different subsetevery time. Doing this is cheap and has much of the same benefit.

Evaluating Our Model

How well does our model do?

Well, first let's figure out where we predicted the correct label. tf.argmaxis an extremely useful function which gives you the index of the highest entryin a tensor along some axis. For example, tf.argmax(y,1) is the label ourmodel thinks is most likely for each input, while tf.argmax(y_,1) is thecorrect label. We can use tf.equal to check if our prediction matches thetruth.

correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))

That gives us a list of booleans. To determine what fraction are correct, wecast to floating point numbers and then take the mean. For example,[True, False, True, True] would become [1,0,1,1] which would become 0.75.

accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

Finally, we ask for our accuracy on our test data.

print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))

This should be about 92%.

Is that good? Well, not really. In fact, it's pretty bad. This is because we'reusing a very simple model. With some small changes, we can get to 97%. The bestmodels can get to over 99.7% accuracy! (For more information, have a look atthislist of results.)

What matters is that we learned from this model. Still, if you're feeling a bitdown about these results, check outthe next tutorial where we do a lotbetter, and learn how to build more sophisticated models using TensorFlow!